Most experts think the FP algorithm usually works better for XRF ANALYZER uses. This is true when you need good accuracy and trust the results. Studies show that the coefficients of determination for important elements like Fe, Al, and Si are above 0.85. The relative standard deviations are less than 10%. This means the results are very precise. Things like how long you measure, the weather, and the sample surface can change the results. So, using longer count times and checking more spots can make the results more reliable.
Key Takeaways
The FP algorithm is very accurate and flexible. It works well with unknown or layered samples. It also works with complex samples. It needs fewer calibration standards.
The Empirical Coefficient Method is good for regular tests. It works best with samples you know well. It needs many matching standards. It also needs careful calibration.
Using both methods together makes results better. This is true for complex samples. It gives lab-level accuracy and trust.
You must prepare samples and calibrate them well. This is important for both algorithms. It helps give good XRF analysis results.
Pick the FP algorithm for fast and flexible field work. Use the Empirical method for careful lab tests with steady samples.
Which Is Better?
Quick Answer
Choosing between the FP algorithm and the Empirical Coefficient Method depends on what you need. Most experts say the FP algorithm gives better accuracy and is more reliable for many XRF ANALYZER jobs. The FP algorithm uses physical models to fix matrix effects. It can work with many types of samples. The Empirical Coefficient Method is good for routine tests when the sample matrix stays the same.
A study by Ytsma et al. (2025) looked at the FP approach and empirical multivariate analysis with many geological standards. The study found that empirical models, especially those with advanced regression, can predict almost as well as FP calibrations. These models are also better at finding low amounts of elements. But the study used machine learning, not the usual Empirical Coefficient Method. So, even though empirical ways can work well, the FP algorithm is still the main choice for most XRF uses.
Tip: If you want flexibility and accuracy with different samples, the FP algorithm is usually the best pick.
Key Factors
Some important things affect which algorithm works best for XRF analysis. Users should think about these before picking one:
Getting the right amount of elements like iron, copper, zinc, and potassium is needed for good results.
XRF analysis helps find small amounts of elements in things like solar cells or living tissues.
Measuring elements the right way lets scientists connect the data to material properties.
The table below shows key performance metrics and how they affect XRF algorithm results:
Performance Metric / Factor | Description / Impact on XRF Algorithm Outcomes |
|---|---|
Resolution | Needed to tell elemental peaks apart; advanced digital signal processors (DSPs) make this better |
Line Shape | Helps spot and measure peaks; DSPs make line shape better and cut down errors |
Throughput Rate | High count rates need DSPs that can handle pile-up and dead time to keep data good |
Background Reduction | DSPs lower background noise, making signals clearer and easier to detect |
Pile-up Recognition | Finding and removing pile-up events stops errors and wrong measurements |
Handling of Rejected Events | Saving rejected events in a different spectrum helps check quality and improve calibration |
Calibration Procedures | Needed to fix system mistakes and database errors |
Spectral Dependent Correction | Changes for detector response and spectral features are needed for correct measurements |
Detector Response Function | Knowing how the detector responds (like a Gaussian peak with tailing) helps read spectra right |
Detector Tailing | Fixing tailing from the detector and electronics makes results more accurate |
Signal Processor Parameter Optimization | DSP settings must be set right because they change how measurements turn out |
Users should also keep these things in mind:
Calibration is very important for both algorithms.
Advanced digital signal processors help make resolution better and lower background noise.
Handling rejected events and pile-up the right way makes data more trustworthy.
When picking between the FP algorithm and the Empirical Coefficient Method, users should match the algorithm to their sample, how accurate they need to be, and what calibration tools they have. Picking the right one gives better results and makes you trust your XRF ANALYZER data more.
FP Algorithm Basics

How It Works
The FP algorithm uses physics and math to find out how much of each element is in a sample. First, it measures the X-rays that come out when a beam hits the sample. Then, it uses known physical constants to figure out the amount of each element. These constants show how X-rays react with different elements. The FP algorithm fixes matrix effects, which are changes caused by other elements in the sample. Because of this, it can work with many types of samples, even if their makeup is different.
The FP algorithm does not need many standards for calibration. It uses physical laws and just a few reference samples. This makes it flexible for different materials. Scientists use the FP algorithm in a modern XRF ANALYZER to get results that are fast and accurate.
The table below shows how the FP algorithm got better in real tests. The numbers show higher accuracy and better linearity for important elements:
Element | Slope (Pre-production) | R2 (Pre-production) | Slope (Final production) | R2 (Final production) |
|---|---|---|---|---|
As | ~1.00 | 0.999 | ~1.03 | 1.000 |
Cd | ~1.05 | 1.000 | ~1.06 | 1.000 |
Hg | ~1.12 | 1.000 | ~1.11 | 1.000 |
Pb | ~1.02 | 0.999 | ~1.05 | 1.000 |
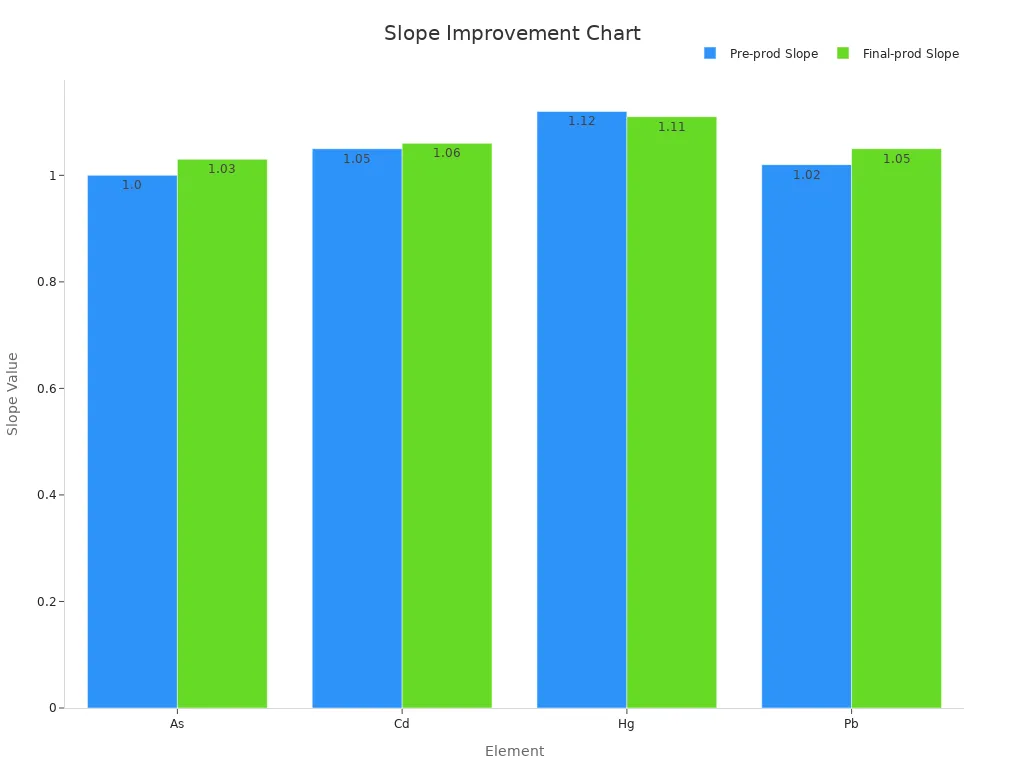
These results show the FP algorithm gives more accurate and reliable measurements after it was improved.
Pros and Cons
The FP algorithm has many strengths for XRF analysis:
It gives good precision, with relative uncertainty for thin films usually between 1% and 10%.
It can measure many elements at once, even in samples with many layers or parts.
It needs less calibration than other methods, so it saves time and effort.
It works well even if your first guess about the sample is not perfect.
But the FP algorithm also has some limits:
It does not give statistical confidence intervals for its results.
It cannot directly check thin samples if you do not know their thickness.
It only works for elemental compositions, not for compounds.
For some special cases, like very thin films, other methods may work better.
The table below sums up the main advantages and limits:
Metric / Aspect | Advantage / Strength | Limitation / Weakness |
|---|---|---|
Relative uncertainty for thin films | 1–10%, good for multi-layer samples | N/A |
Concentration accuracy | About 0.4% over full range | N/A |
Computational cost | Low | N/A |
Sensitivity to initial estimates | Not sensitive | N/A |
Statistical confidence intervals | N/A | Not provided |
Sample thickness analysis | N/A | Cannot analyze unknown thickness |
Composition handling | N/A | Only for elements, not compounds |
Comparison with other methods | Can combine with least squares for better results | Least squares needs more computing and is sensitive to starting values |
Validation with other techniques | Matches well with profilometry and SEM | N/A |
Note: The FP algorithm matches well with other measurement methods, like profilometry and SEM, if you know the sample’s density. This agreement means you can trust the FP algorithm’s results in many real-world cases.
Empirical Coefficient Method
How It Works
The Empirical Coefficient Method uses real measurements from standards to make a calibration curve. Scientists measure X-ray intensity from samples with known element amounts. They plot these numbers and use linear regression to draw a line that links intensity to concentration. The equation often looks like this:Y = MX + E
where Y is the measured intensity, M is the slope, X is the concentration, and E is the intercept.
To get good results, scientists follow several steps. They measure intensities from standards with known element amounts. They make a calibration curve using the data they collect. They use intensity counts, background levels, and calibration numbers like slope and intercept as important statistics. They add correction factors to fix matrix effects and interferences. They prepare samples carefully and sometimes use a sample spinner to make the sample more even. They think about how deep the X-rays go and how thick the sample is. They compare unknown samples to the saved calibration curve to find the concentration.
This method works well for many geological materials, like volcanic rocks and obsidian. It helps the XRF ANALYZER give results that are close to those from lab-based methods.
Pros and Cons
The Empirical Coefficient Method has both strengths and weaknesses. It gives good accuracy and repeatability when the sample type matches the calibration standards. The method uses influence coefficients to fix matrix effects and overlapping peaks, like when zirconium and strontium signals overlap. This correction makes the data better.
A table below shows key findings about this method:
Statistical Parameter | Key Finding | Implication for Empirical Coefficient Method Effectiveness |
|---|---|---|
Precision (Repeatability) | RSD gets better up to 180 seconds count time but does not improve much after that | Makes measurement repeatability better without needing longer count times |
Accuracy | pXRF data matches data from other analytical methods | Gives accuracy like lab techniques |
Reliability (Reproducibility) | No big improvement after 180 seconds count time | Keeps reproducibility steady in real situations |
Calibration Approach | Using influence coefficients fixes matrix effects and secondary X-ray enhancements | Helps with complex sample matrix problems, making data better |
Application Scope | Works well for many geological materials | Shows it can be used for many types of samples |
But the method has some limits. Calibration curves can be simple (linear) or more complex (polynomial). Linear curves are easy but can be affected by outliers. Polynomial curves fit better but can break easily. Outliers, like a high zirconium value, can change results. Removing them makes accuracy better but makes the range smaller. Overlapping peaks can cause mistakes if not fixed. The method depends on how even the sample is and how good the reference standards are. It cannot predict results for samples outside the calibration range. Instrument settings and sample preparation must stay the same.
Note: The Empirical Coefficient Method makes results more similar between instruments but cannot handle unknown or out-of-range samples well. It works best for routine analysis with known sample types.
XRF Analyzer Algorithms Compared
Accuracy
The FP algorithm gives high accuracy for many samples. It uses physical laws to fix matrix effects. This helps it measure elements in mixed samples. The Empirical Coefficient Method can also be accurate. But it only works well if the sample matches the standards. If the sample is different, the results may not be as good.
Scientists learned that using both the FP algorithm and empirical calibration together helps even more. For example, when testing gold alloys, this combined method worked very well. The measured and certified values matched almost perfectly (R² = 0.9999). The relative error was less than 0.1%. This means the combined way can be as good as or better than lab methods for some elements.
When you need the best accuracy, the FP algorithm or a combined method is usually best. This is true for unknown or mixed samples.
Calibration
Calibration is important for both algorithms. The FP algorithm only needs a few reference samples. It uses physical constants, so it is easier to set up for new materials. The Empirical Coefficient Method needs many standards that are just like the samples. If the standards do not match, calibration will not work well.
The table below shows how calibration changes the results:
Calibration Aspect | FP Alone (No Calibration) | FP + Empirical Calibration | Notes/Comments |
|---|---|---|---|
Correlation (R²) | N/A | 0.9999 | Very high correlation between certified values and EDXRF measurements |
Relative Error (rel%) | 0.5 to 1.5 wt% | < 0.1% | Significant reduction in relative error after combining FP with empirical calibration |
Absolute Error (wt%) | 0.5 to 1.5 wt% | < 0.27 wt% | Improvement in gold assay accuracy with compatible calibration materials and software |
Relative Standard Deviation (%rsd) | N/A | <0.11% (pure Au) | Slightly higher for Au-Ag and Au-Cu alloys (0.16% and <0.20%) after K-factor correction |
Statistical Test (Student t-test) | N/A | Confirmed equivalence | EDXRF precision equivalent to fire assay method, validating combined calibration approach |
Correction Method | N/A | K-factor correction applied | Corrects systematic measurement errors due to alloy mixtures |
The table shows that using both calibration methods lowers errors. It also makes the results more trustworthy. The FP algorithm alone already has low errors. Adding empirical calibration makes it even better.
Ease of Use
The FP algorithm is easy to use for many samples. Users do not need to make lots of standards. They can get results fast, even if they do not know much about the sample. Most XRF ANALYZER software helps users step by step.
The Empirical Coefficient Method takes more work. Users must make and measure many standards. They also have to keep the instrument settings and sample prep the same every time. If anything changes, they might need to redo calibration. This takes more time and effort, especially for new or unknown samples.
For the same type of sample, the Empirical Coefficient Method can be simple. For new or changing samples, the FP algorithm saves time and helps avoid mistakes.
Flexibility
The FP algorithm works with many sample types. It can handle unknown materials, mixtures, and layered samples. Users can test different samples without making new calibration curves each time. This makes the FP algorithm very flexible.
The Empirical Coefficient Method works best when the sample matches the standards. If the sample changes, users must make new calibration curves. This makes it less useful for unknown or complex samples.
A quick comparison:
FP Algorithm
Handles matrix effects well
Needs less calibration
Works for unknown and complex samples
Needs some understanding of physical models
Empirical Coefficient Method
Works best for routine, known samples
Needs many standards for each sample type
Not good for unknown or changing samples
Simple math, but less flexible
To sum up, the FP algorithm is more flexible and accurate for most XRF ANALYZER jobs. The Empirical Coefficient Method is good for routine work with stable samples.
Real-World Use
Industrial Cases
Many companies use XRF analysis to fix real problems. In Changchun, China, a group checked city soil for heavy metals using portable XRF. They worked in a busy area with lots of factories. The group used a special math model to fix the XRF data. This made their results as good as lab tests. They could check many places fast and spot pollution right away. This shows XRF algorithms help with quick, big checks.
Another example is from Portugal. Scientists looked at soil near old coal mines. They used advanced math with XRF data to find metals like arsenic and lead. Their method gave strong results, with R² values from 0.79 to 0.99 for different elements. These high numbers mean XRF analysis worked well, even in dirty places. The right algorithm made the XRF ANALYZER a strong tool for industry and the environment.
Lab and Field
Researchers also test XRF algorithms in labs and outside. In one study, teams used portable XRF on old glass from archaeological sites. Even though the machines were different, they got similar results by fixing the FP data. When they had only a few standards, they used ratio corrections. With more standards, they used linear regression. This made the results better and helped compare data from different labs.
In another lab study, scientists tested precious metal alloys. They found empirical methods need many matching standards and smooth sample surfaces. The FP method worked better when standards were missing or samples were not perfect. By using FP with empirical calibration, they got results that matched certified values, with errors under 0.1%. This way made both accuracy and trust better, showing why using both methods helps with complex samples.
Choosing for Your XRF Analyzer
When to Use FP
The FP algorithm is best when you need to test many kinds of samples. It uses physical models, so you do not need lots of calibration standards. It works well with unknown or layered samples. Many companies use the FP algorithm in confocal micro X-ray fluorescence setups. These setups help make 3D maps of elements in layered or structured materials. For example, companies use FP to check multilayer polymer samples with iron fillers. Scientists use FP to study art objects, like painting layers or parchment, without damaging them. Geoscientists use FP to map inclusions in diamonds or minerals. Researchers use FP to track plant nutrients in biological samples. The FP method is also good when it is hard to find reference materials. It works well for samples with light or medium atomic numbers, like polymers or organic materials. Users can trust the FP algorithm for semi-quantitative results, especially when the sample shape is tricky.
Tip: Pick FP if you need to test unknown, layered, or structured samples, or if you do not have matrix-matched standards.
When to Use Empirical
The Empirical Coefficient Method is a good choice for routine tests of samples you know well. This method uses calibration curves made from standards that match the sample matrix. It works well when matrix effects, like secondary fluorescence or absorption, are strong and can be fixed with regression. Studies show empirical methods, like multiple linear regression and chemometric approaches, often work better than FP in complex matrices such as steels, ores, or old glass. Empirical methods handle matrix effects and spectral interferences better if you have enough calibration data. They give high accuracy for samples with complex or mixed matrices, as long as calibration samples match the unknowns. Chemometric methods, like Partial Least Squares, help get better results in tough samples. Users should pick the empirical method when they have many matching standards and need to control matrix effects in complex materials.
Note: Use the empirical method for routine, high-precision work with well-known, complex samples and when you can make enough calibration standards.
Decision Checklist
Use this checklist to help you pick the right algorithm for your XRF ANALYZER:
Are your samples unknown, layered, or structured? → FP
Do you not have matrix-matched calibration standards? → FP
Do you need to test polymers, biological, or art-historical samples? → FP
Are your samples well-known and standards easy to get? → Empirical
Do matrix effects or spectral interferences change your results a lot? → Empirical
Do you need the best accuracy in complex, mixed samples? → Empirical
The FP algorithm is very accurate and works with many samples. The empirical method is best for samples you know well. You should pick the method that fits your sample and what you need. Think about how hard your sample is, what calibration tools you have, and how exact you want to be. Some advanced methods, like TXRF, can find very tiny amounts. They can measure as little as 10⁻¹² grams. This is great for thin films and checking surfaces. The chart below shows that taking more measurements can make errors go down in XRF analysis.
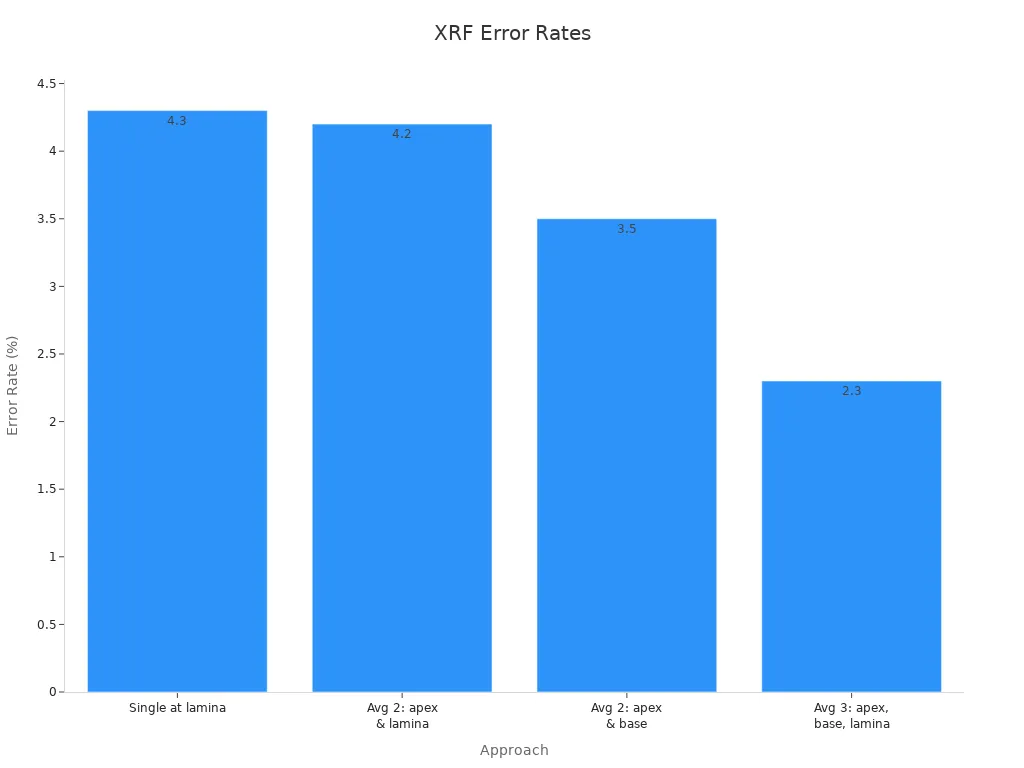
If you want to learn more, you can look at dynamic analysis methods. You can also try open-source software like GeoPIXE.
FAQ
What is the main difference between the FP algorithm and the Empirical Coefficient Method?
The FP algorithm uses physics and math to study samples. The Empirical Coefficient Method uses real measurements from known standards. FP is good for samples you do not know much about. The empirical method works best for samples you already know well.
Can users switch between FP and Empirical methods on the same XRF analyzer?
Most new XRF analyzers let users pick either method. Switching depends on the software and how calibration is set up. Users should look at the analyzer’s manual to learn how to switch.
Why does the FP algorithm need fewer calibration standards?
The FP algorithm uses physical laws and just a few reference samples. It does not need many standards because it figures out results by how X-rays react with elements.
Does sample preparation affect both algorithms?
Yes. Both algorithms work better with clean, flat, and even samples. If you do not prepare samples well, both methods can give wrong results.
Which method is better for field analysis?
The FP algorithm is usually better for field work. It can handle unknown or mixed samples and does not need much calibration. This makes it easier and faster for quick checks outside the lab.






WhatsApp
Scan the QR Code to start a WhatsApp chat with us.